Axel Laborieux

Axel Laborieux

Postdoctoral researcher in Neuro-AI  | PhD in Physics | Polytechnique alumnus (X14)

Publications

Improving equilibrium propagation without weight symmetry through Jacobian homeostasis

Laborieux, A., & Zenke, F., ICLR, 2024

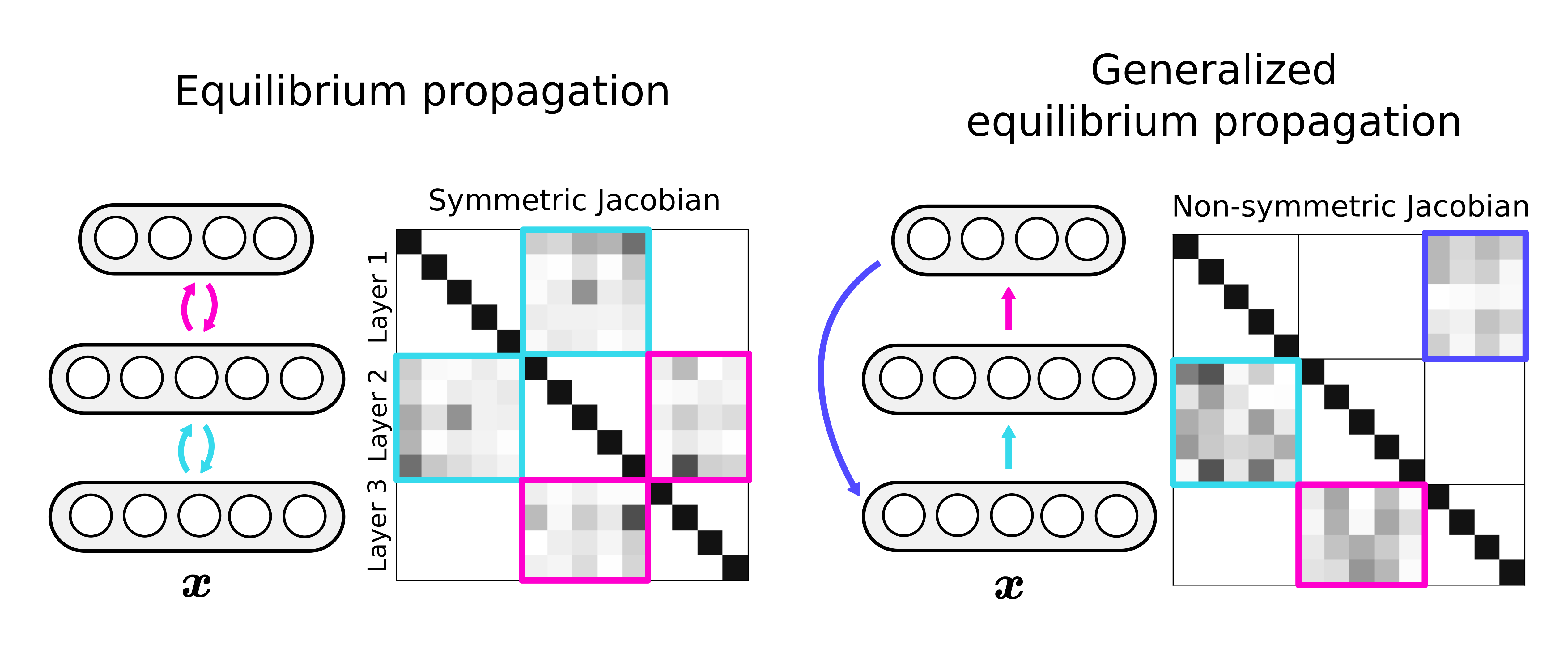
thumbnail

Equilibrium propagation (EP) is a local learning rule with strong theoretical links to gradient-based learning. However, it assumes an energy-based network, which enforces the synaptic connections to be symmetric. This is not only biologically implausible, but also restrictive in terms of architecture design. Here, we extend holomorphic EP to arbitrary converging dynamical systems that may not have an energy function. We quantify how the lack of energy function impacts the accuracy of the gradient estimate, and propose a simple regularization loss that maintains the network’s Jacobian closer to symmetry, which is more general than making the synapses symmetric. These improvements make generalized hEP scale to large scale vision datasets such as ImageNet 32.

( paper | preprint | code )

Implicit variance regularization in non-contrastive SSL

Srinath Halvagal, M.*, Laborieux, A.*, & Zenke, F. (* equal contribution), NeurIPS, 2023

thumbnail

Non contrastive self-supervised learning (SSL) methods learn by making representations invariant to random augmentations of data. However, how the trivial constant output solution (collapse) is avoided remains poorly understood. Building prior theories, we show how non-contrastive SSL might implicitly regularize the variance of learned representation, thereby avoiding collapse. Our theory also suggests new loss functions making learning more robust.

( paper | preprint | code )

Holomorphic equilibrium propagation computes exact gradients through finite size oscillations

Laborieux, A., & Zenke, F., NeurIPS (Oral), 2022

thumbnail

In this paper we extend Equilibrium Propagation to holomorphic networks and show that it can compute the gradient of the loss exactly through finite size neuronal oscillations.

( paper | preprint | code )

Bio-inspired continual learning and credit assignment for neuromorphic computing

Laborieux, A., Université Paris-Saclay, 2021

This is my thesis!

( paper | oral )

Synaptic metaplasticity in binarized neural networks

Laborieux, A., Ernoult, M., Hirtzlin, T., & Querlioz, D., Nature Communications, 2021

thumbnail

In this work we investigate an interesting and previously unexplored link between the optimization process of binarized neural networks (BNNs) and neuroscience theories of synaptic metaplasticity. We show how to modify the training process of BNNs to mitigate forgetting and achieve continual learning.

( paper | code | press )

Scaling equilibrium propagation to deep convnets by drastically reducing its gradient estimator bias

Laborieux, A., Ernoult, M., Scellier, B., Bengio, Y., Grollier, J., & Querlioz, D., Frontiers in Neuroscience, 2021

thumbnail

In this paper we show that Equilibrium Propagation can scale to more complex tasks

( paper | preprint | code )

Implementation of ternary weights with resistive RAM using a single sense operation per synapse

Laborieux, A., Bocquet, M., Hirtzlin, T., Klein, J. O., Nowak, E., Vianello, E., Portal, J.-M., & Querlioz, D., TCAS I, 2020

This is an extended version of our AICAS 2020 paper where we further validate or approach against device variations

( paper | preprint | code )

Low power in-memory implementation of ternary neural networks with resistive RAM-based synapse

Laborieux, A., Bocquet, M., Hirtzlin, T., Klein, J. O., Diez, L. H., Nowak, E., Vianello, E., Portal, J.-M., & Querlioz, D., AICAS, 2020

In this paper we show how to implement a ternary artificial synapse for edge-AI applications

( paper | preprint | code | award )